Cinemática vetorial

Cinemática Vetorial

Na Cinemática Escalar, estudamos a descrição de um movimento em trajetória conhecida, utilizando as grandezas escalares. Agora, veremos como obter e correlacionar as grandezas vetoriais descritivas de um movimento, mesmo que não sejam conhecidas previamente as trajetórias.
Grandezas Escalares – Ficam perfeitamente definidas por seus valores numéricos acompanhados das respectivas unidades de medida. Exemplos: massa, temperatura, volume, densidade, comprimento, etc.
Grandezas vetoriais – Exigem, além do valor numérico e da unidade de medida, uma direção e um sentido para que fiquem completamente determinadas. Exemplos: deslocamento, velocidade, aceleração, força, etc.

VETORES

Para representar as grandezas vetoriais, são utilizados os vetores: entes matemáticos abstratos caracterizados por um módulo, por uma direção e por um sentido.
Representação de um vetor – Graficamente, um vetor é representado por um segmento orientado de reta: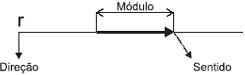 

Elementos de um vetor:
Direção – Dada pela reta suporte (r) do vetor.
Módulo – Dado pelo comprimento do vetor.
Sentido – Dado pela orientação do segmento.
Resultante de vetores (vetor-soma) – Considere um automóvel deslocando-se de A para B e, em seguida, para C. O efeito desses dois deslocamentos 
combinados é levar o carro de A para C. Dizemos, então, que o vetor é a soma ou resultante dos vetores e . 

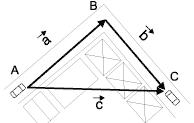
Regra do Polígono – Para determinar a resultantedos vetores e , traçamos, como na figura acima, os vetores de modo que a origem de um coincida com a extremidade do outro. O vetor que une a origem de com a extremidade de é o resultante .
Regra do paralelogramo – Os vetores são dispostos de modo que suas origens coincidam. Traçando-se um paralelogramo, que tenhae como lados, a resultante será dada pela diagonal que parte da origem comum dos dois vetores.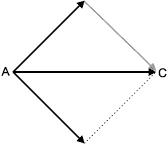 

Componentes ortogonais de um vetor – A componente de um vetor, segundo uma dada direção, é a projeção ortogonal (perpendicular) do vetor naquela direção. Decompondo-se um vetor , encontramos suas componentes retangulares, _x e _y, que conjuntamente podem substituí-lo, ou seja, = _x + _y.

Adição de Vetores

Podemos somar dois ou mais vetores, para obter um vetor soma. 
Regra do polígono: 
Ligam-se os vetores origem com extremidade. O vetor soma é o que tem origem na origem do 1º vetor e extremidade na extremidade do último vetor.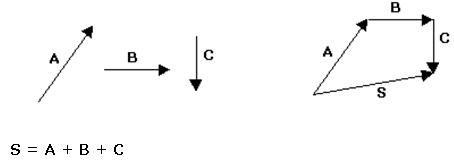 

Subtração de Vetores 

Para subtrair dois vetores adicionamos um deles ao oposto do outro.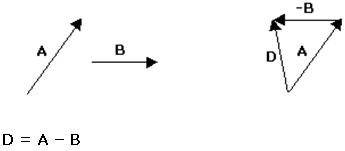

Vetor x Número Real
O produto de um número real n por um vetor A, resulta em um vetor R com sentido igual ao de A se n for positivo ou sentido oposto ao de A se n for negativo. O módulo do vetor R é igual a n x |A|.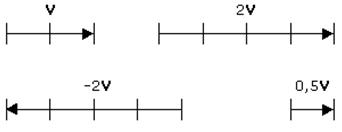

Decomposição de Vetores
A decomposição de vetores é usada para facilitar o cálculo do vetor resultante.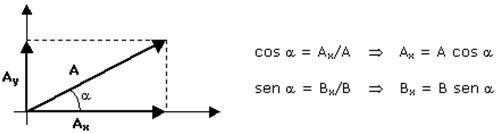

Seja um vetor R resultado da seguinte operação: R = A + B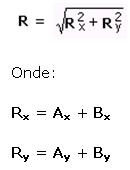

_A e _B = vetores-posição (vetores com origem em O, ponto de referência arbitrariamente escolhido, com extremidade no lugar em que está o móvel e com módulo igual à distância que o separa da origem.
Se um móvel realizar um movimento de A para B, terá realizado um deslocamento (grandeza vetorial ), com origem no ponto A e extremidade no B, dado pela diferença entre o vetor-posição no fim do deslocamento (_B) e o vetor-posição no início (_A):
=_A -_B

VELOCIDADE VETORIAL MÉDIA

Numa trajetória qualquer (retilínea ou curvilínea), a velocidade vetorial média é definida pela razão entre o vetor deslocamento e o correspondente intervalo de tempo: 

(o vetor velocidade média tem a mesma direção e o mesmo sentido do vetor deslocamento).
Aplicação
01. Num instante t₁, um carro de Fórmula 1 encontra-se a 600m ao norte em relação ao box de sua equipe e, 20s depois, a 800m a oeste do mesmo referencial. Determinar o módulo do deslocamento vetorial (r) e o módulo da velocidade vetorial média do carro (v_m) entre esses dois instantes.
Aplicação
Solução: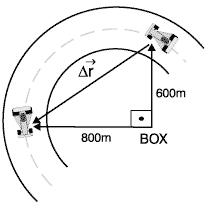

Pelo Teorema de Pitágoras, calculamos o módulo do deslocamento escalar: 

VELOCIDADE VETORIAL INSTANTÂNEA
A direção, o sentido e a “rapidez” (módulo) do movimento, em cada ponto da trajetória, são os elementos que o vetor velocidade instantânea representa.
Em um movimento retilíneo:
A velocidade vetorial, em dado instante, tem o sentido do movimento e a direção da reta em que ele ocorre: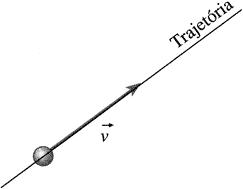 

Em um movimento curvilíneo:
A velocidade vetorial instantânea tem direção tangente à curva, no ponto considerado, e sentido indicado pela orientação do vetor: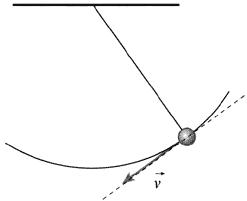 

Importante: uma grandeza vetorial só é constante se forem constantes sua direção, seu sentido e sua intensidade. Assim, o único movimento que tem velocidade vetorial constante é o movimento retilíneo e uniforme.

 

ACELERAÇÃO VETORIAL INSTANTÂNEA

É a aceleração vetorial de um móvel em cada ponto de sua trajetória.
Como todo vetor pode ser obtido pela soma de suas componentes perpendiculares, vamos decompor o vetor aceleração instantânea, tomando como base a direção do vetor velocidade: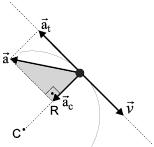 

a) Aceleração tangencial (_t) – É a componente da aceleração vetorial na direção do vetor velocidade ( ) e indica a variação do módulo deste. Possui módulo 
igual ao da aceleração escalar: 

Importante:
1) Em movimentos acelerados, _t e têm o mesmo sentido.
2) Em movimentos retardados, _t e têm sentidos contrários, como na figura anterior.
3) Em movimentos uniformes, _t é nula, já que o módulo de não varia nesses movimentos.
b) Aceleração centrípeta ou normal (c) – É a componente da aceleração vetorial na direção do raio de curvatura (R) e indica a variação da direção do vetor velocidade (). Tem sentido apontando para o centro da trajetória (por isso, centrípeta) e módulo
dado por: 

Importante: nos movimentos retilíneos,_c é nula porque o móvel não muda de direção nesses movimentos.
Aceleração vetorial resultante – A obtenção da intensidade da aceleração resultante pode ser feita aplicando-se o Teorema de Pitágoras no triângulo retângulo em destaque na figura:
a₂ = a²_t + a²_c