D E S C R I Ç Ã O
Notação científica padronizada
A definição básica de notação científica permite uma infinidade de representações para cada valor. Mas a notação científica padronizada inclui uma restrição: a mantissa (coeficiente) deve ser maior ou igual a 1 e menor que 10. Desse modo cada número é representado de uma única maneira.
Como transformar
Para transformar um número qualquer para a notação científica padronizada devemos deslocar a vírgula obedecendo ao princípio de equilíbrio.
Vejamos o exemplo abaixo:
A notação científica padronizada exige que a mantissa (coeficiente) esteja entre 1 e 10. Nessa situação, o valor adequado seria 2,5375642 (observe que a sequência de algarismos é a mesma, somente foi alterada a posição da vírgula). Para o exponente, vale o princípio de equilíbrio: "Cada casa decimal que diminui o valor da mantissa aumenta o expoente em uma unidade, e vice-versa".
Nesse caso, o expoente é 5.
Observe a transformação passo a passo:


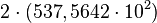
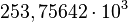
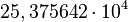

Um outro exemplo, com valor menor que 1:
0,0000000475
0,000000475 × 10−1
0,00000475 × 10−2
0,0000475 × 10−3
0,000475 × 10−4
0,00475 × 10−5
0,0475 × 10−6
0,475 × 10−7
4,75 × 10−8
Operações
Adição e subtração
Para somar ou subtrair dois números em notação científica, é necessário que os expoentes sejam o mesmo. Ou seja, um dos valores deve ser transformado para que seu expoente seja igual ao do outro. A transformação segue o mesmo princípio de equilíbrio. O resultado possivelmente não estará na forma padronizada, sendo convertido posteriormente.
Exemplos:

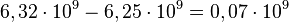 (não padronizado)
(não padronizado) 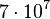 (padronizado)
(padronizado)
Multiplicação
Multiplicamos as mantissas e somamos os expoentes de cada valor. O resultado possivelmente não será padronizado, mas pode ser convertido.
Exemplos:
 (não padronizado)
(não padronizado)  (convertido para a notação padronizada)
(convertido para a notação padronizada)
 (já padronizado sem necessidade de conversão)
(já padronizado sem necessidade de conversão)
Dividimos as mantissas e subtraímos os expoentes de cada valor. O resultado possivelmente não será padronizado, mas pode ser convertido:
Exemplos:
 (padronizado)
(padronizado)
 (não padronizado)
(não padronizado) 
Exponenciação
A mantissa é elevada ao expoente externo e o congruente da base dez é multiplicado pelo expoente externo.
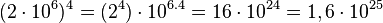 (padronizado)
(padronizado)
Radiciação
Antes de fazer a radiciação é preciso transformar um expoente para um valor múltiplo do índice. Após feito isso, o resultado é a radiciação da mantissa multiplicada por dez elevado à razão entre o expoente e o índice do radical.

![\sqrt[5]{6,7\cdot 10^{17}} = \sqrt[5]{670\cdot 10^{15}} = \sqrt[5]{670}\cdot 10^{15/5} \approx 3,674\cdot 10^{3}](http://upload.wikimedia.org/math/5/f/4/5f4091fa9076fe7b68fdae63b176b459.png)
Outros Exemplos:
Multiplicação
a x 10m . b x 10n = a . b x 10( m + n )
a) 5 x 105 . 3 x 108 = 5 . 3 x 10(5 + 8) = 15 x 1013 = 1,5 x 1014
b) 2 . 5 x1011 = 2 x 100 . 5 x 1011 = 2 . 5 x 10(0 + 11) = 10 x 1011 = 1 x 1012
c) 3 x 1012 . 7 x 10-13 = 3 . 7 x 10(12 - 13) = 21 x 10-1 = 2,1 x 100 = 2,1
Divisão
a x 10m / b x 10n = a / b x 10( m - n )
a) 7 x 1013 / 5 x 107 = ( 7/5 ) x 10(13 - 7) = 1,4 x 106
b) 4 x 107 / 2 = 4 x 107 / 2 x 100 = (4/2) x 10(7 - 0) = 2 x 107
c) 3 / 7 x 1011 = 3 x 100 / 7 x 1011 = (3/7) x 10(0 - 11) = 0,43 x 10-11 = 4,3 x 10-12
d) 5 x 10-3 / 8 x 109 = (5/8) x 10(-3 - 9) = 0,62 x 10-12 = 6,2 x 10-13
e) 2 x 10-5 / 3 x10-3 = (2/3) x 10(-5 - (-3)) = 0,67 x 10(-5 + 3) = 0,67 x 10-2 = 6,7 x 10-3
Potenciação
(a x 10n)m = am x 10(n . m)
a) (5 x 10-3)2 = 52 x 102(-3) = 25 x 10-6 = 2,5 x 10-5
b) (7 x 107)3 = 73 x 107.3 = 343 x 1021 = 3,43 x 1023
Radiciação
m√ a x 10n = m√ a x 10n/m
a) 3√ 3 x 10-3 = 3√ 3 x 10-3/3 = 1,44 x 10-1
b) 2√ 7 x 1012 = 2√ 7 x 1012/2 = 2,6 x 106
Adição e subtração
Colocar os valores na mesma potência de base 10. Colocar esta potência em evidência.
a) 1 x 103 + 1 x 104 = 1 x 103 + 10 x 103 = (1 + 10) x 103 = 11 x 103 = 1,1 x 104
b) 3 x 10-3 + 7 x 10-4 = 3 x 10-3 + 0,7 x 10-3 = (3 + 0,7) x 10-3 = 3,7 x 10-3





3 comentários:
eu gostaria de saber qual a importância da notação cientifica e no que ela é utilizada...obrigada
eu queria saber qual é a importancia da notação cientifica para o aluno.obrigada
A notação científica é bastante usada para cálculos aonde os valores ão elevados. É uma outra forma de apresentar os números.
Postar um comentário